定义：

平面内到两个定点F1,F2的距离之和等于一个常数（大于|F1F2|）的点的轨迹叫做椭圆

这两个定点叫做焦点

两定点间的距离叫做焦距

标准方程:

方程形式1:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$

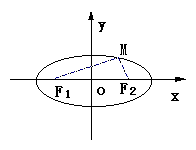
焦点:

$F_1(-c,0), F_2(c,0)$

方程形式2:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$

焦点：

$F_1(0,c), F_2(0,-c)$

焦距：

$|F_1F_2| = 2c$

$c=\sqrt{a^2-b^2}$

几何性质：

范围：

$|x| \le a, |y| \le b$
所以在由直线$x=\pm a, y=\pm b$围成的矩形内

对称性：

坐标轴是椭圆的对称轴，原点是椭圆的对称中心。
椭圆的对称中心叫做椭圆的中心。

顶点：

$A_1(-a,0), A_2(a,0), B_1(0,-b), B_2(0,b)$ 叫做椭圆的顶点

$A_1A_2$ 叫长轴

$B_1B_2$ 叫短轴

长半轴为$a$,短半向为$b$

离心率：

$e=\frac{c}{a} (0<e<1)$

$e$越接近$1$，椭圆越扁；$e$越接近$0$，椭圆越接近于圆。