三位数学家
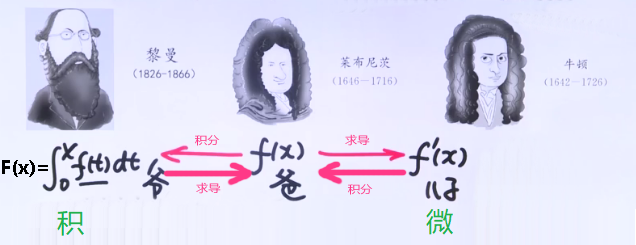
- 函数及其性质是高等数学整个基础知识的核心问题;
- 上图中的“爷、爸、儿子”仅为帮助大家方便记忆起的称呼哟,可不是真正的祖孙三代 ^_^;
注:
三个人物的时间关系:Leibniz 1646(记住这个年份,就可以推出旁边两位的时间)出生的前4年是牛顿,牛顿1726去世之后的100年是黎曼;
人物简介:
莱布尼茨(Gottfried Wilhelm Leibniz; 高教出版社通常翻译为莱布尼茨cí,但是大家还是喜欢翻译为:莱布尼兹zī 因为Leibniz的最后一个音z的缘故。) 是函数f(x) 提出者的代表;
[老师→学生 之间的关系]:
莱布尼茨 → 约翰·伯努利 → 洛必达(买来的 二流子) 、欧拉 → 拉格朗日 → 柯西;
牛顿(Isaac Newton)是莱布尼茨的老对头,他提出了f′(x)导数(即对函数f(x)求导)的概念;
[老师→学生 之间的关系]:
牛顿 → 泰勒+麦克劳林;
注: 牛顿和莱布尼茨刚开始是好朋友,好到穿一条裤子,年轻时互通有无,功成名就之时彻底翻脸,老死不相往来;
黎曼(Georg Friedrich Bernhard Riemann.德国人,19世纪无人能够企及的数学分析大师)提出了∫0xf(t)dt积分的概念;
微积分:
微积分不仅研究f(x)函数本身,还研究它的f′(x)导数(叫 微分),还要研究它的积分(叫 积分学)。为了方便记忆,我们把∫0xf(t)dt,f(x),f′(x)这三个都叫做“祖孙三代”;
通过具体例子来理解上面抽象的“祖孙三代”:
我们假设y=f(x)=sinx,那么对其求导就是cosx,对其积分就是1−cosx
为了方便区分,我们再对sinx积分时将其中的x换为t:
∫0xsintdt=−cost∣0x=−(cosx−cos0)=−(cosx−1)=1−cosx
“祖孙三代”的图像如下:
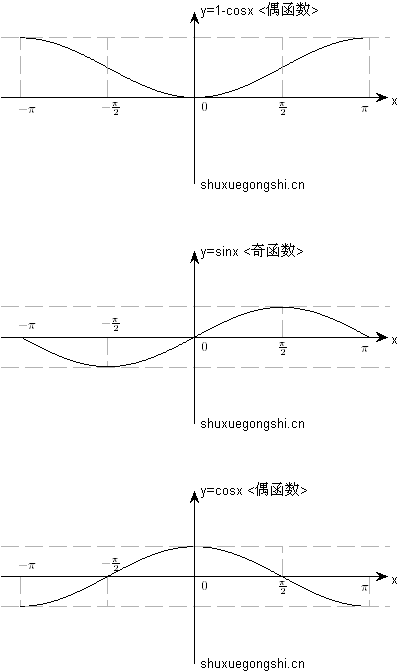
上图的解释:
- y=1-cosx的画法,可以先将y=cosx的图像的y值取反,然后再向上平移1个单位;
- 图像从上往下看,下面函数是上面函数求导所得;
图像从下往上看,上面函数是下面函数积分所得; - 奇函数必过原点(0,0),且关于原点(0,0)对称;
偶函数关于y轴对称;
小结:
- 191003 ★
求导或积分之后,奇偶性互换(即:导一次,奇偶性换一次;导一次,奇偶性换一次),周期性不变(即:如果原函数是周期性函数,那么求导之后,还是周期性函数且周期性不变); - ★
祖孙三代函数及其性质;
总结 ★
1. 前提:奇偶函数的定义域必须关于原点对称;
2. 奇偶函数的基本类型如下所示:(7个小点)
I. f(x)+f(−x)∈ 偶函数
E.g 1)y=2ex+e−x∈偶函数,图像如下: //悬链线(女孩戴的项链)、 双曲余弦; 伯努利研究出来的哟;
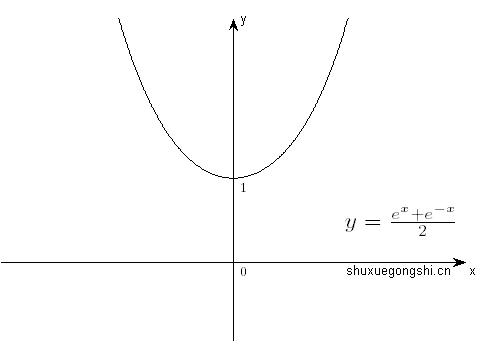
2) y=3(1+x)2+3(1−x)2
∈偶函数,图像如下(该图像的正确性有待考证):
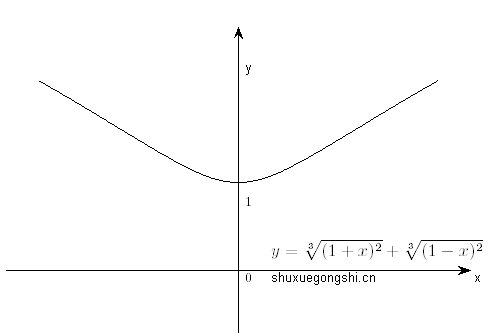
II. f(x)−f(−x)∈ 奇函数
E.g 1)y=2ex−e−x∈奇函数,图像如下: //双曲正弦
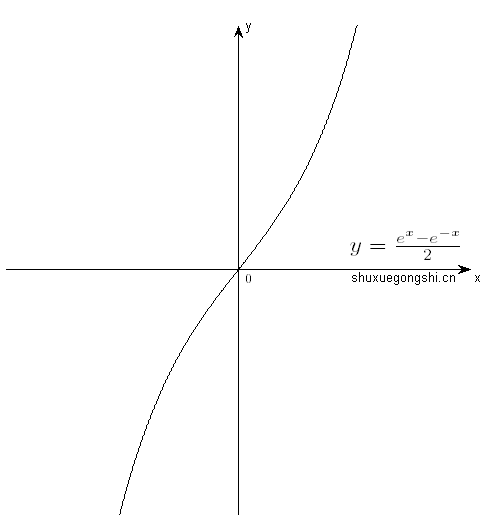
2)y=ln1−x1+x∈奇函数,图像如下(该图像的正确性有待考证):
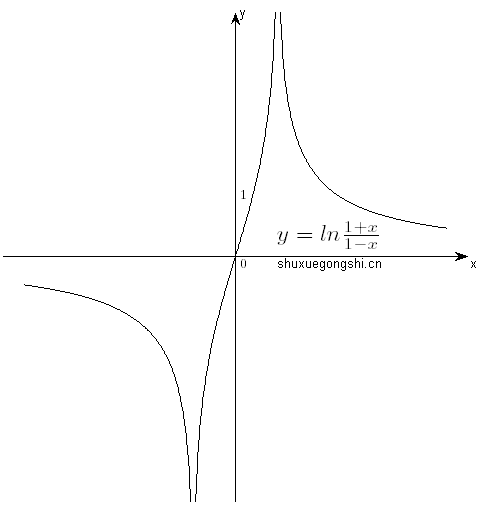
III. f[φ(x)]复合函数的奇偶性情况:
奇[偶] ⇒ 偶
内偶外奇必为偶;
E.g y=sinx2,内层函数u=x2是偶函数,外层函数y=sinu是奇函数,那么复合之后就是偶函数;
偶[奇] ⇒ 偶
内奇外偶必为偶
E.g y=cos(sinx),内层函数u=sinx是奇函数,外层函数y=cosu是偶函数,那么复合之后就是偶函数;
y=∣sinx∣,内层函数u=sinx是奇函数,外层函数y=∣u∣是偶函数,那么复合之后就是偶函数;
奇[奇] ⇒ 奇
内奇外奇必为奇
E.g y=sinx1,内层函数u=x1是奇函数,外层函数y=sinu是奇函数,那么复合之后就是奇函数;
y=3tanx
,内层函数u=tanx是奇函数,外层函数y=3u
是奇函数,那么复合之后就是奇函数;
偶[偶] ⇒ 偶
内偶外偶必为偶
E.g y=cos∣x∣,内层函数u=∣x∣是偶函数,外层函数y=cosu是偶函数,那么复合之后就是偶函数;
y=∣cosx∣,内层函数u=cosx是偶函数,外层函数y=∣u∣是偶函数,那么复合之后就是偶函数;
非[偶] ⇒ 偶
内偶外非必为偶
E.g y=ex2,内层函数u=x2是偶函数,外层函数y=eu既不是奇函数也不是偶函数,那么复合之后是偶函数;
y=ln∣x∣,内层函数u=∣x∣是偶函数,外层函数y=lnu既不是奇函数也不是偶函数,那么复合之后是偶函数;
III的记忆:
从上面可以知道,只要内外有一个有偶,则最终肯定为偶函数;
IV. 一个特殊的函数: ln(x+x2+1
)∈ 奇函数,它的函数图像如下: //反双曲正弦(因为它的图形正好和上面的双曲正弦看着和y=x对称^^)

注:
因为 x+x2+1
忽略其中的1之后,即:x+x2
≈x+∣x∣,
而 x+∣x∣⩾0 //即:任何一个数 加 自己的绝对值 都是 非负的,
所以 ln(x+x2+1
) 的 x+x2+1
⩾0,
即 x可以是任何数啦,即:x∈(−∞,+∞);
V. 求导之后,奇偶性互换; //即前面的小结部分
f(x)奇 ⇒f′(x) 偶 ⇒f′′(x) 奇 ⇒ …
f(x)偶 ⇒f′(x) 奇 ⇒f′′(x) 偶 ⇒ …
VI. 积分之后,奇偶性互换; //即前面的小结部分
注意:积分是0下限;
f(x) 奇 ⇒∫0xf(t)dt 偶
f(x) 偶 ⇒∫0xf(t)dt 奇
VII. ★ f(x)连续, ∀x,y
f(x+y)=f(x)+f(y)⇒f(x)∈奇函数
E.g
取y=0 f(x)=f(x)+f(0)⇒f(0)=0
取y=-x f(0)=f(x)+f(−x)⇒f(x)=−f(−x)
3. 变体类型 //平移
I. f(x) 偶函数 ⇒ 关于y轴(x=0)对称: f(0+x)=f(0−x)
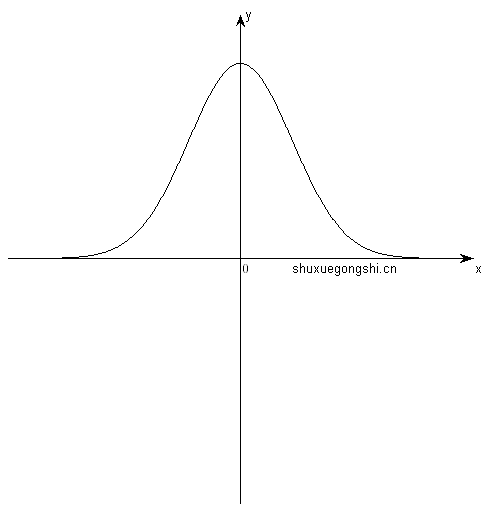
//平移
⇒ 关于x=T对称: f(T+x)=f(T−x)
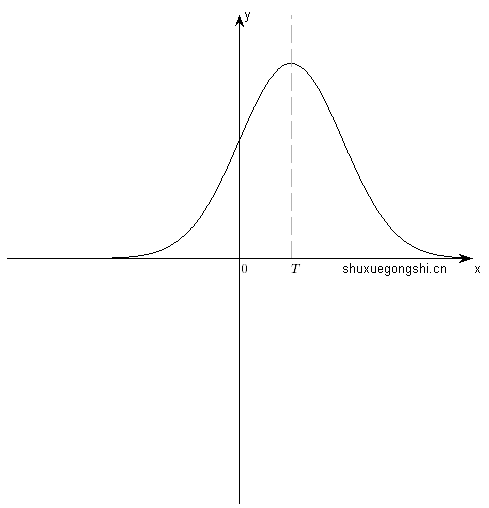
II. f(x) 奇函数 ⇒ 关于原点(0,0)对称:
//平移
f(x) 奇函数 ⇒ 关于原点(x0,0)对称:

技巧:
记住结论,使用结论!!!
来源: 宇哥的微博
https://weibo.com/tv/v/H92Eu4WXn
https://weibo.com/tv/v/H93tTg8ie










