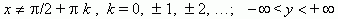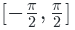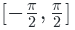三角函数的图像和性质：

正弦函数 和 余弦函数

函数 y=sinx y=cosx
图像

正弦函数

余弦函数
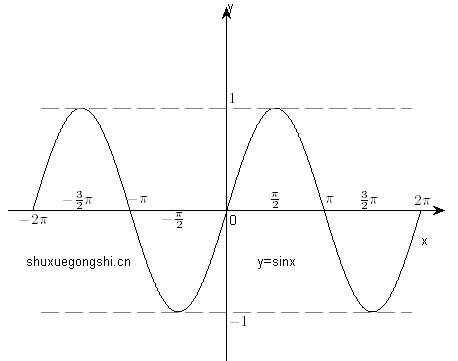
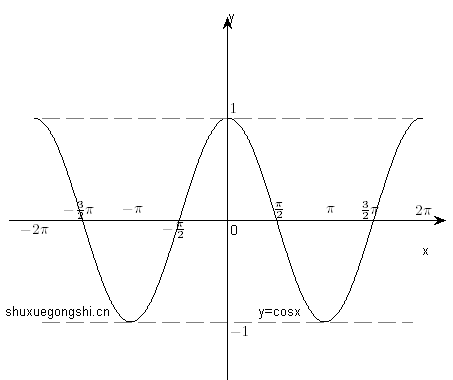
定义域 (-∞,+∞) (-∞,+∞)
值域 [-1,1] [-1,1]
奇偶性 奇函数 偶函数
周期性 是周期函数,2π是最小正周期 是周期函数,2π是最小正周期
有界性 |sinx|≤1 |cosx|≤1

常用的函数值:
sin0=0,sinπ6=12,sinπ4=22,sinπ3=32,sinπ2=1 sin0=0, sinfrac{pi}{6}=frac{1}{2}, sinfrac{pi}{4}=frac{sqrt{2}}{2}, sinfrac{pi}{3}=frac{sqrt{3}}{2} , sinfrac{pi}{2}=1
cos0=1,cosπ6=32,cosπ4=22,cosπ3=12,cosπ2=0,cosπ=−1 cos0=1, cosfrac{pi}{6}=frac{sqrt3}{2}, cosfrac{pi}{4}=frac{sqrt{2}}{2}, cosfrac{pi}{3}=frac{1}{2} , cosfrac{pi}{2}=0, cos{pi}=-1

正切函数 和 余切函数：

函数 y=tanx y=cotx
图像
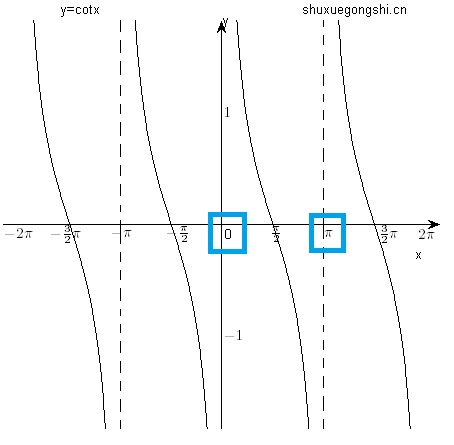定义域
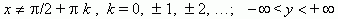值域 (-∞,+∞) (-∞,+∞)
奇偶性 奇函数 奇函数
周期性 是周期函数,π是最小正周期 是周期函数,π是最小正周期

常用的函数值:
tan0=0,tanπ6=33,tanπ4=1,tanπ3=3,tanπ=0 tan0=0, tanfrac{pi}{6}=frac{sqrt{3}}{3}, tanfrac{pi}{4}=1,tanfrac{pi}{3}=sqrt3, tanpi=0
cotπ2=0,cotπ6=3,cotπ4=1,cotπ3=33 cotfrac{pi}{2}=0, cotfrac{pi}{6}=sqrt{3}, cotfrac{pi}{4}=1, cotfrac{pi}{3}=frac{sqrt{3}}{3}

反三角函数的图像和性质：

函数 y=arcsinx y=arccosx
图像
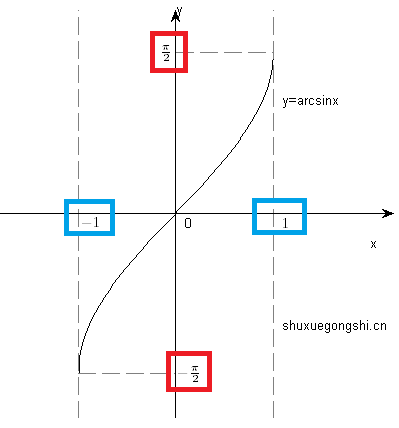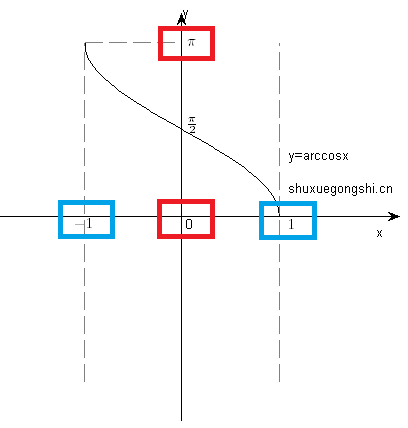定义域 [-1,1] [-1,1]
值域
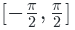奇偶性 奇函数 非奇非偶
周期性 无 无
单调性 单调增加 单调减少

常用的函数值:
arcsin0=0,arcsin12=π6,arcsin22=π4,arcsin32=π3,arcsin1=π2arcsin0=0, arcsinfrac{1}{2}=frac{pi}{6}, arcsinfrac{sqrt{2}}{2}=frac{pi}{4}, arcsinfrac{sqrt{3}}{2}=frac{pi}{3}, arcsin1=frac{pi}{2}
arccos1=0,arccos32=π6,arccos22=π4,arccos12=π3,arccos0=π2arccos1=0, arccosfrac{sqrt{3}}{2}=frac{pi}{6}, arccosfrac{sqrt{2}}{2}=frac{pi}{4}, arccosfrac{1}{2}=frac{pi}{3}, arccos0=frac{pi}{2}

函数 y=arctanx y=arccotx
图像
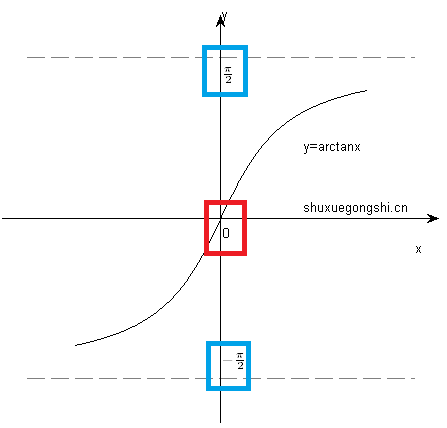定义域 (-∞,+∞) (-∞,+∞)
值域
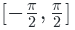奇偶性 奇函数 非奇非偶
周期性 无 无
单调性 单调增加 单调减少

关于arccotx的图像，使用不同的数学软件可能绘制的不同，这一点请参见文章<Which is the correct graph of arccot x?>

常用的函数值:
arctan0=0,arctan33=π6,arctan1=π4,arctan3=π3arctan0=0, arctanfrac{sqrt{3}}{3}=frac{pi}{6}, arctan1=frac{pi}{4}, arctansqrt{3}=frac{pi}{3}
arccot0=π2,arccot3=π6,arccot1=π4,arccot33=π3arccot0=frac{pi}{2}, arccotsqrt{3}=frac{pi}{6}, arccot1=frac{pi}{4}, arccotfrac{sqrt{3}}{3}=frac{pi}{3}