一、该模型的定理描述

如果两个三角形的高相等，那么它们的面积之比就等于它们的底边长之比。

用字母表示就是：

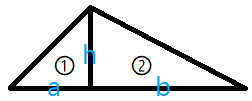
假设：
三角形①的底边是 $a$，面积为$S1$，
三角形②的底边是 $b$，面积为$S2$，
它们的高都是 $h$。
那么：

$\frac{S1}{S2} = \frac{a}{b}$

二、为什么？（直观理解与推导）

三角形的面积公式是：$\text{面积} = \frac{1}{2} \times \text{底} \times \text{高}$

1. 三角形①的面积：

$S_1 = \frac{1}{2} \times a \times h$

2. 三角形②的面积：

$S_2 = \frac{1}{2} \times b \times h$

现在，让我们计算它们的面积比：
$\frac{S_1}{S_2} = \frac{\frac{1}{2} \times a \times h}{\frac{1}{2} \times b \times h}$

你会发现，等式右边的 $\frac{1}{2}$ 和 $h$ 是完全相同的，所以它们可以“抵消掉”（约分）。最后就剩下：
$\frac{S_1}{S_2} = \frac{a}{b}$

这就好比说： 两个三角形共用一条“高”，就像两块用同样高度的橡皮泥捏成的“长条”。那么哪块橡皮泥更大（面积更大），就只取决于它的“底边”更长了。底边是几倍关系，面积就是几倍关系。

三、常见图形模型（非常重要！）

这个定理在几种经典图形中应用极广：

模型1：等高模型（基础）

两个三角形并排摆放，拥有相同的高。

    A
   /|\
  / | \
 /  |  \
B---D---C

在三角形ABC中，如果D是BC边上的点，那么 $\triangle ABD$ 和$\triangle ADC$的高都是从A点向BC所作的垂线，所以它们是等高的。
因此：$\frac{S_{\triangle ABD}}{S_{\triangle ADC}} = \frac{BD}{DC}$

模型2：梯形中的蝴蝶模型

在梯形中，对角线相交后形成的左右两个三角形（“翅膀”）面积相等，其证明就用到了等高模型。

模型3：沙漏模型

利用平行线间的等高特性，产生多组面积比等于底边比的三角形。

四、总结与应用

你可以把这个定理记成一个简单的口诀：

“高相等，面积比等于底边比。” //★★★

在做几何题时，一旦你发现两个三角形拥有“公共高”或“相等的高”，就要立刻想到这个定理，它能把复杂的面积问题转化为简单的线段比例问题，是解题的一把利器。