一、该模型的定理描述
如果两个三角形的底边相等,那么它们的面积之比就等于它们的高的之比。
用字母表示就是:
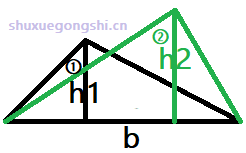
假设:
黑色三角形①的高是 ,面积为,
绿色三角形②的高是 ,面积为,
黑色三角形①和绿色三角形②有公共的底边 ,
那么:
二、为什么?(推导过程)
同样从面积公式出发:
- 三角形①的面积:
- 三角形②的面积:
计算面积比:
等式右边的 ( \frac{1}{2} ) 和底边 ( b ) 是完全相同的,所以它们可以“抵消掉”(约分)。最后就剩下:
直观理解: 这就像是用同一根橡皮筋(底边相同)撑出两个三角形。那么哪个三角形被撑得更高(高更大),哪个面积就更大。高是几倍关系,面积就是几倍关系。
三、常见图形模型
这个定理最经典的应用场景是“平行线间的等积变形”。
模型:夹在平行线间的同底三角形
直线L1 _____A_____________D____
/ \ / \
/ \ / \
/ \ / \
直线L2 __/_______\_____/_______\__
B C B C( 和 拥有公共底边 BC,并且顶点 A 和 D 在另一条平行于 BC 的直线上移动)
- 因为直线 L1 // 直线 L2,所以平行线间的距离(也就是高)是固定的。
- 因此,△ABC 和 △DBC 不仅同底(BC),而且等高!
- 根据这个定理,它们的面积相等。
结论: 夹在一组平行线之间,且同底的三角形,面积必然相等。这个原理常用于图形的“等积变形”,是求解复杂面积问题的重要技巧。
