方法1：解方程

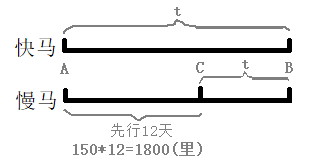
分析 - 图1


分析：
1.慢马先行12天，走的路程sac=vt=15012=1800s_{ac}=vt=15012=1800里；
2.然后快马开始追赶，此时快马从A到B 和 慢马从C到B 所用的时间相同为 tt;
3.根据题意，快马追上慢马时，相遇在B点，所以快马和慢马所走的路程相同都为sabs_{ab}:
快马:sab=240s_{ab}=240t
慢马:sab=sac+scb=15012+150ts_{ab}=s_{ac}+s_{cb} = 15012+150t
所以， 240t=1800+150t⇒(240−150)t=1800⇒90t=1800⇒t=20240t=1800+150t \Rightarrow (240-150)t=1800 \Rightarrow 90t=1800 \Rightarrow t=20

方法2：纯算术

1. 慢马先走的路程

慢马每天行 150 里，先走 12 天，先走的路程是：
150×12=1800 里 150 \times 12 = 1800 \ \text{里}

2. 快马追赶的速度差

快马每天比慢马多走：
240−150=90 里240 - 150 = 90 \ \text{里}
这个“90 里/天”就是快马追上慢马的速度。

3. 追及时间

追及时间 = 路程差 ÷ 速度差
1800÷90=20 天1800 \div 90 = 20 \ \text{天}

最终答案：

快马需要 20 天追上慢马。

所用的小学数学知识点分析

  1. 整数乘法
    计算慢马先行路程：150×12=1800150 \times 12 = 1800

  2. 整数减法
    求速度差：240−150=90240 - 150 = 90 。

  3. 整数除法
    求追及时间：1800÷90=20 1800 \div 90 = 20。

  4. 追及问题基本模型
    理解核心公式：追及时间 = 初始距离 ÷ 速度差。
    理解“速度差”的含义：快马比慢马每天多追回的距离。

  5. 等量关系与一步解应用题的思路
    将文字题转化为数学计算步骤，先求路程差，再求速度差，最后相除得时间。

这道题是典型的“追及问题”，只涉及整数的四则运算，是小学三、四年级常见的行程应用题类型，也体现了古代数学的智慧。