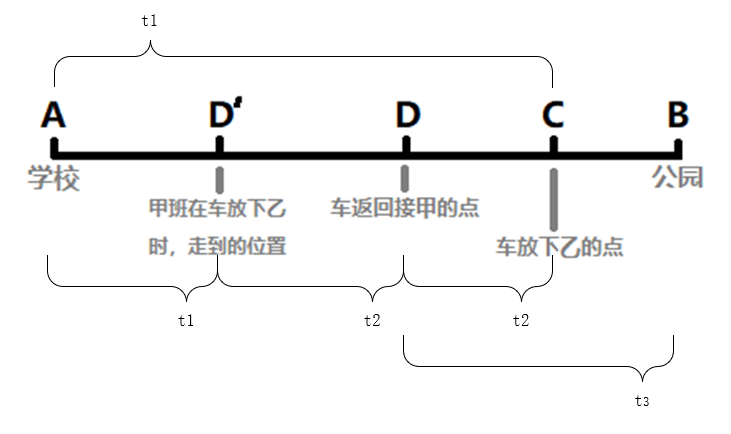
1. 明确过程与符号

• 学校 A，公园 B，$S_{AB} = 54$ km

• 校车速度 $v_c = 45$ km/h，步行速度 $v_w = 5$ km/h

• 乙班先乘车，甲班先步行

• 车到 C 点放下乙班（乙步行至 B），此时甲班走到 $D^{'}$;
  然后车返回在 D 点接甲班（甲在 D 点乘车至 B），车在返回过程中甲班继续从$D^{'}$往B点步行，甲班和返回的车相遇在D点；

• 两班同时到达 B

设：

• $t_1$ = 车从 A 到 C 的时间（乙乘车时间）

• $t_2$ = 车从 C 返回遇到D 点甲班的时间

• $t_3$ = 车从 D 到 B 的时间（甲最后一段乘车时间）

2. 第一阶段

第一阶段（0 ~ $t_1$）

• $S_{AC} = 45 t_1$

• 甲班步行距离 $S_{AD^{'}} = 5 t_1$（D’ 是 $t_1$ 时刻甲的位置）

3. 第二阶段

第二阶段（返回相遇，时长 $t_2$）

在 $t_1$ 时刻：

• 车在 C，甲在 D’，相距 $S_{CD^{'}} = S_{AC} - S_{AD^{'}} = 45 t_1 - 5 t_1 = 40 t_1$ km

• 车返回，甲继续向前，相对速度 $45 + 5 = 50$ km/h

• 相遇时间 $t_2 = \frac{S_{CD^{'}}}{50}= \frac{40 t_1}{50} = 0.8 t_1$

相遇点 D 的位置：

• 甲从 A 到 D 的总时间 = $t_1 + t_2 = t_1 + 0.8 t_1 = 1.8 t_1$

• $S_{AD} = 5 \times 1.8 t_1 = 9 t_1$ km

4. 第三阶段

第三阶段（最后一段，时长 $t_3$）

甲班：
$S_{DB} = S_{AB} - S_{AD} = 54 - 9 t_1$ km
甲乘车 DB 时间：$t_3 = \frac{54 - 9 t_1}{45}$

乙班：
$S_{CB} = S_{AB} - S_{AC} = 54 - 45 t_1$ km
乙步行 CB 时间：$t_{3'} = \frac{54 - 45 t_1}{5}$

5. 求总时间

甲班总时间 = 乙班总时间。

甲班总时间 = $t_1 + t_2 + t_3$
乙班总时间 = $t_1 + t_{3'}$

所以：

$t_1 + t_2 + t_3 = t_1 + t_{3'}$

$t_2 + t_3 = t_{3'}$

代入 $t_2 = 0.8 t_1$，$t_3 = \frac{54 - 9 t_1}{45}$，$t_{3'} = \frac{54 - 45 t_1}{5}$：

$0.8 t_1 + \frac{54 - 9 t_1}{45} = \frac{54 - 45 t_1}{5}$

两边乘 45：
$36 t_1 + 54 - 9 t_1 = 9 (54 - 45 t_1)$
$27 t_1 + 54 = 486 - 405 t_1$
$27 t_1 + 405 t_1 = 486 - 54$
$432 t_1 = 432$
$t_1 = 1 \ \text{小时}$

$t_2 = 0.8 \times 1=0.8$

$t_3 = \frac{54 - 9 t_1}{45} = \frac{54- 9 \times 1}{45} = \frac{45}{45} = 1$

6. 重新计算总时间

甲班总时间检查：
$S_{AD} = 9 t_1 = 9$km，步行时间 = 9 / 5 = 1.8 小时（即 $t_1 + t_2 = 1 + 0.8 = 1.8$ 小时，一致）
$S_{DB} = 54 - 9 = 45$ km，乘车时间 = 45 / 45 = 1 小时
甲总时间 = 1.8 + 1 = 2.8 小时，一致。

乙班总时间 = $t_1 + t_{3'}$
AC = 45×1 = 45 km，CB = 54 - 45 = 9 km
$t_{3'} = \frac{9}{5} = 1.8$ 小时
总时间 = $1 + 1.8 = 2.8$ 小时

最终答案：

两个班的学生用最短的时间同时到达公园需要 2.8 小时。