1. 画图理解题意

分析 - 图1

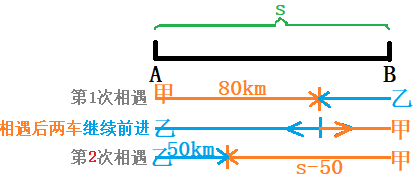
  • A、B两城之间距离设为 s s 千米。

  • 第1次相遇：在离A城80千米处，即甲车走了80千米。
    此时两车共走的路程和 = s s （一个全程）。

  • 到第2次相遇：两车共走了 3s 3s （三个全程）。

  • 第2次相遇点离A城50千米，说明甲车从A到B再返回到离A 50千米处。

2. 分析甲车的总路程

分析：(真对本题此分析无作用,只是常规分析)
第1步：
因为第1次相遇的时候，甲和乙走的时间相同(t甲=t乙t_{\text{甲}} = t_{\text{乙}}):
t甲=s甲v甲t_{\text{甲}} = \frac{s_\text{甲}}{v_\text{甲}}
t乙=s乙v乙t_{\text{乙}} = \frac{s_\text{乙}}{v_\text{乙}}
⇒\Rightarrow
v甲v乙=s甲s乙=80s−80\frac{v_\text{甲}}{v_\text{乙}} = \frac{s_\text{甲}}{s_\text{乙}} = \frac{80}{s-80}
其中:
s甲=80,s乙=s−80s_{\text{甲}}=80 , s_{\text{乙}}=s-80

从开始到第2次相遇，两车共走 3s 3s 千米，因为速度不变，所以每辆车走的路程都是第1次相遇时所走路程的3倍。
所以：

  • 甲车第一次相遇时走了 80 km。
  • 到第二次相遇时，甲车总共走了 80×3=240km。

3. 用第二次相遇位置，求 s

分析 - 图2


甲车从A出发到第二次相遇的路线：
甲先从A到B（走了 s s 千米），再从B返回向A走了某段，相遇时离A 50千米，说明甲返回时已经走了 s−50 s - 50 千米（从B向A方向算，B到相遇点距离 = s−50 s - 50 ）。

那么甲的总路程 = s+(s−50)=2s−50 s + (s - 50) = 2s - 50 。

上面已知甲总路程 = 240 千米，所以：
2s−50=2402s - 50 = 240
2s=2902s = 290
s=145s = 145

4. 检验

第一次相遇：离A 80千米，即甲走80，乙走 145−80=65 145 - 80 = 65 千米，速度比 80:65=16:13 80:65 = 16:13 。

到第二次相遇：总路程 3×145=435 3 \times 145 = 435 千米，甲走 435×1629=240 435 \times \frac{16}{29} = 240 千米（符合），乙走195千米。

甲具体路线：A→B：145千米，B返回走 240−145=95 240 - 145 = 95 千米，相遇点离B 95千米，离A 145−95=50 145 - 95 = 50 千米，符合题意。

最终答案：

A、B两城相距145千米。

所用的小学数学知识点分析

  1. 相遇问题基本公式
    路程和 = 速度和 × 时间。
    第一次相遇路程和 = 1个全程，第二次相遇路程和 = 3个全程。

  2. 比例思想
    第一次相遇时两车路程比等于速度比，且速度比不变，所以走3个全程时甲的路程是走1个全程时的3倍。

  3. 乘法与解方程

    80 \times 3 = 240 是乘法；

    2S - 50 = 240 是一元一次方程，用逆运算求解。

  4. 线段图分析能力
    理解“离A城50千米”在第二次相遇时表示甲车已经走过全程并返回了一段。

  5. 检验意识
    得出答案后可以验证速度比与路程是否一致。

这道题是典型的多次相遇问题，考查比例、线段图与方程的结合，是小学高年级行程问题的经典题型。